Le modèle de Black-Scholes pour l’évaluation d’une option, avec un exemple numérique

Lorsqu’en 1973, Fisher Black, Myron Scholes et Robert Merton publient leurs travaux sur la façon de couvrir une option grâce à la détention du sous-jacent et du cash, afin de construire un portefeuille sans risque, tout en donnant une formule d’évaluation des options, ils ne s’attendent peut être pas à rester dans les annales de la finance. Le modèle peut s’appliquer à un actif suivant un processus stochastique. En 1997, Merton et Scholes se voient finalement récompensés par le prix Nobel d’économie (Black ne pouvait être éligible car décédé en 1995).

Aujourd’hui, le modèle de Black-Scholes, bien que souvent décrié, est considéré comme une avancée fondamentale pour la finance moderne. En quoi consiste leur modèle ? Découvrons tout simplement leur formule, ainsi qu’un exemple numérique.

Une formule d’évaluation des options relativement simple en apparence

La formule de Black-Scholes (1973) peut être utilisée pour évaluer une option européenne ne payant pas de dividendes. Pour une option d’achat (call) et une option de vente (put), les formules sont les suivantes :

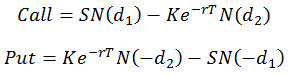
Où :

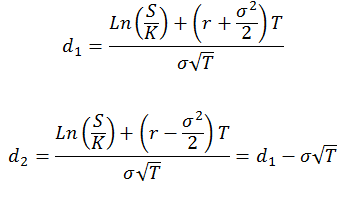
Avec :

La formule de Black-Scholes, à travers un exemple numérique

Maintenant que l’on connaît la formule de Black Scholes, on peut l’appliquer à l’évaluation d’un call européen par exemple.

Soit un call sur Arcelourd, une entreprise spécialisée dans le commerce de l’acier, dont les résultats futurs semblent prometteurs. L’action vaut aujourd’hui 80 euros. Soit un call de strike 90 et de maturité un trimestre. Les taux d’intérêts sans risque pour cette période sont équivalents à 5%. La volatilité implicite est estimée à 35%. Donc, S = 80, K = 90, T = 0,25, r = 0,05, σ = 0,35.

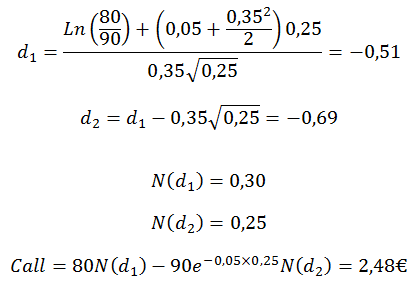
Jusqu’ici, cette option a été évaluée sans dividendes. Il est possible de les intégrer dans la formule de Black Scholes assez simplement.

Finance de Marché est un site d’information grand public, ayant pour vocation de partager les connaissances liées aux thématiques financières. Pour en savoir plus, pour des demandes de partenariat ou autre, n'hésitez pas à nous contacter.

Catégories : Finance, Généraliste | Tags : Black & Scholes, Options | 2 commentaires