Variance Swap : définition & payoff d’un produit de volatilité
Un trader d’option peut être amené à couvrir son risque de volatilité. Il peut le faire soit en prenant une position inverse sur d’autres options pour annihiler son vega, soit directement à travers des produits basés directement sur la volatilité, tels que des Variance ou Volatility Swap. Un spéculateur peut, quant à lui, directement prendre une position sur la volatilité d’un sous-jacent.
Le Variance Swap : Définition
Le Variance Swap (VarSwap) est un contrat permettant d’échanger un montant de variance réalisée sur un laps de temps donné, contre un montant de variance fixé à l’avance. L’échange se fait selon la formule suivante :
S’agissant d’un swap, aucun flux n’est échangé en date initial. A maturité, si la volatilité réalisée est supérieure à la volatilité strikée, le vendeur du VarSwap paie le montant décrit par l’équation ci-dessus. Si la volatilité réalisée est inférieure à la volatilité strikée, le vendeur du VarSwap reçoit le montant décrit par l’équation ci-dessus.
Pour un VarSwap où l’investisseur est acheteur de volatilité, les flux potentiels sont les suivants :
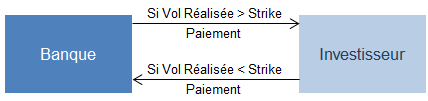
Le Variance Swap, un exemple de calcul
Sans entrer dans les méthodes de construction du VarSwap, il convient de définir les différents termes de l’équation pour comprendre quel est le montant exact de l’échange à maturité.
Variance Notional. Il s’agit du montant de la transaction. Celui-ci est égal à :
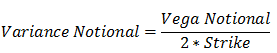
Avec cette convention, si la volatilité réalisée est supérieure d’un point à la volatilité strikée, le profit du VarSwap est approximativement égal au Vega Notional (pour une volatilité réalisée assez proche du strike). Les traders s’expriment donc en Vega Notional car il s’agit d’une mesure permettant de calculer plus rapidement le profit potentiel à tirer d’une telle transaction.
Exemple : prenons un VarSwap 1 an sur le S&P500, avec un Vega Notional de 100,000 USD, et un Strike de 12%. Si, dans un an, la volatilité réalisée est de 13%, l’investisseur reçoit un montant proche de (13 – 12) * 100,000 = 100,000 :
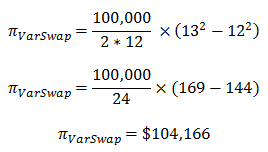
Realized Vol. La volatilité d’un sous-jacent est définie de plusieurs façons mathématiques. On sait qu’il s’agit de l’écart type, c’est-à-dire de la propension d’un élément à s’écarter de sa moyenne. Pour un VarSwap, la définition de la volatilité réalisée est la suivante :
Avec :
– St = niveau du sous-jacent en date t
– N = nombre d’observations (jours de trading)
Strike. Il s’agit tout simplement du montant de volatilité accordée entre les deux contreparties avant d’entrer dans la transaction. Il s’agira de la référence du swap.
Le cap du Variance Swap à 2,5
Généralement, les VarSwap sont échangés avec un cap de 2,5x sur la volatilité réalisée. Ceci est dû au risque de convexité évident dans le calcul d’une volatilité. En effet, sans cap, un investisseur étant short vol peut théoriquement perdre une somme infinie (σ2), il n’existe pas de borne supérieure mais simplement une borne inférieure (0). Par exemple, pour un VarSwap avec un strike de 30, la plus haute volatilité réalisée observable dans le contrat sera 30 x 2,5 = 75. Le facteur de 2,5 n’a pas réellement de fondement mathématique, il s’agit simplement d’une convention adoptée par les traders sur le marché.
Utilisation de Variance Swap pour construire des Trades de dispersion
Les Variance Swaps sont également connus pour leur rôle dans les trades de dispersion où l’investisseur prend une vue sur la corrélation entre un indice et ses sous-jacents. Généralement, l’investisseur souhaite être short correlation. Pour cela, il achète des variance swaps sur chacun des constituants d’un indice et vend un variance swap sur l’indice lui-même.


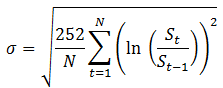
tres bonne explication : simple et efficace.
merci