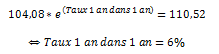Comment calculer les taux forward à partir des taux zéro-coupon ? Définition & exemple

La courbe des taux zéro-coupon contient de nombreuses informations sur les taux qui prévaudraient dans le futur. On peut en effet déduire, à partir des taux zéro-coupon de différentes échéances, les fameux taux forward. Ceci peut être particulièrement utile pour les investisseurs, qui peuvent alors constater les attentes du marché en matière de taux d’intérêts futurs, et prendre par exemple certaines décisions de trésorerie ou de d’investissement. Vaut-il mieux investir à long terme ou répéter son opération plusieurs fois ? Peut-on attendre avant de s’endetter ? Comment calculer les taux forward ?

Calcul du taux forward : exemple simple

Supposons qu’un investisseur soit confronté à un taux zéro-coupon 1 an de 4% et à un taux zéro-coupon 2 ans de 5%. On en déduit qu’un investissement de 100€ dans une obligation 1 an zéro-coupon croîtra jusqu’à devenir l’équivalent de 100 * e^0,04 = 104,08€. De même, 100€ placés dans une obligation 2 ans zéro-coupon donneront 100 * e^{0,05 * 2} = 110,52€. La question que doit se poser l’investisseur est la suivante : si, à la fin d’un investissement d’un an, il investissait à un nouveau pour une période d’un an, quel serait le taux auquel il aurait droit pour ce second investissement ? La réponse doit satisfaire l’égalité :

En d’autres termes, investir 100€ à 4% pour une première période d’un an, puis réinvestir la somme obtenue à 6%, équivaut à placer son argent deux ans d’affilée à 5%. Le taux de 6% est ce qu’on appelle le Taux forward_{1 an dans 1 an}.

Calcul du taux forward : généralisation

Imaginons que les taux zéro-coupon pour des échéances plus longues soient également connus.

On peut déduire, par la même méthode, les taux forward ultérieurs. Par exemple, le taux forward 1 an dans 2 ans est celui qui permettrait de satisfaire :

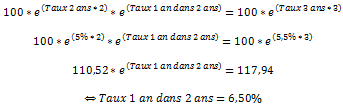
Comment généraliser le calcul du taux forward ? On peut utiliser la formule suivante :

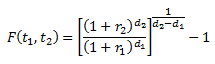
Avec :
– F(t₁, t₂) : taux forward entre t₁ et t₂
– r₁ : taux zéro-coupon d’échéance t₁
– r₂ : taux zéro-coupon d’échéance t₂
– d₁ : nombre d’années entre la date initiale et l’échéance t₁
– d₂ : nombre d’années entre la date initiale et l’échéance t₂

Calcul du taux forward : quelle décision pour ma trésorerie ?

Imaginons que vous soyez à la tête d’une entreprise et que votre directeur financier vous demande d’évaluer la possibilité d’émettre de la dette, afin d’effectuer quelques acquisitions au cours des prochaines années. Le taux zéro-coupon 1 an est de 5%. Le taux zéro-coupon 2 ans est de 5,50%. En revanche, le taux forward 1 an dans 1 an de 6%, déduit à travers les deux taux précédents, vous semble trop élevé. Quelle décision prendre quant à votre endettement ?

Si vous pensez que, dans un an, le taux zéro-coupon qui prévaudra sera en-dessous de 6%, vous devriez alors :

– Emettre une dette à court terme, et payer 5% sur une échéance d’un an
– Puis émettre à nouveau de la dette dans un an, et payer le taux zéro-coupon qui prévaudra alors

Si la courbe zéro-coupon dans un an est la même qu’aujourd’hui, vous aurez alors raison et pourrez émettre à nouveau de la dette pour 5% sur un an. Le taux moyen payé sera donc bien de 5%.

En s’endettant directement sur deux ans, à 5,50%, vous ne profiteriez pas d’une baisse des taux zéro-coupon.

Finance de Marché est un site d’information grand public, ayant pour vocation de partager les connaissances liées aux thématiques financières. Pour en savoir plus, pour des demandes de partenariat ou autre, n'hésitez pas à nous contacter.

Catégories : Finance, Généraliste | Tags : Forward | Publiez votre commentaire