Delta d’une option à la monnaie : pourquoi est-il égal à 0,5 ?
Le delta d’une option, ∆, représente la sensibilité du prix de cette dernière face à un changement de prix du sous-jacent. Il s’agit de la pente de la courbe reliant la valeur de l’option au cours de l’action. Chacun sait que le delta d’un call à la monnaie vaut 0,5. En d’autres termes, si l’action augmente de 1 euros, le prix d’une option d’achat à la monnaie augmentera de 0,5 euros. Mais pourquoi ?
Le delta d’une option à la monnaie, un calcul simplifié
Adoptions un raisonnement simplifié (parmi tant d’autres). Pour rappel, le delta est défini mathématiquement comme suit :
Et l’on sait que pour un call, il est équivalent à :
N étant la fonction de répartition de la loi normale centrée réduite, et d1 étant lui-même équivalent à :
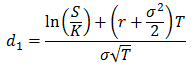
Que se passe-t-il lorsque l’option est à la monnaie ?
Dans ce cas, K = S. D’où :
d1 devient alors :
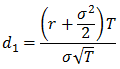
Le taux d’intérêt, r, est négligeable, car voisin de zéro (il ne s’élèvera dans la réalité qu’à quelques pourcents, 0,0x).
d1 devient donc :
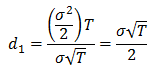
Pour une action, la volatilité implicite du sous-jacent, σ, sera probablement de l’ordre de quelques dizaines de pourcent, donc inférieur à 1. Pour une option relativement courte, le temps, T, sera inférieur à 1 puisqu’il est exprimé en nombre d’années. En d’autres termes, le numérateur sera très probablement voisin de zéro. Par exemple, pour une volatilité implicite de 20% et une maturité de trois mois, d1 deviendrait égal à 0,2 * 0,25 / 2 = 0,025, soit une valeur très proche de zéro.
Or, nous savons que N(d1) est la fonction de répartition de la loi normale centrée réduite, qui va de 0 à 1 en valeur. N(0+) prend donc une valeur proche de 0,5+.
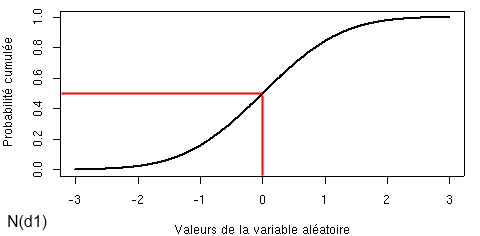
Connaître le delta d’une option, c’est donc tout simplement avoir en tête l’allure de la fonction de répartition de la loi normale centrée réduite, qui n’est pas des plus compliquées !
