Comment calculer le prix d’une option à partir d’un arbre binomial simple ? Exemple numérique
Une alternative intéressante au modèle de Black-Scholes, dans le cadre de la valorisation d’options, est l’utilisation d’arbres binomiaux. Cette méthode a été décrite par Cox, Ross et Rubinstein en 1979. Elle consiste à déterminer le prix d’une option à partir des différentes trajectoires que peut prendre le sous-jacent. Comment calculer le prix d’une option à partir d’un arbre binomial simple ? Exemple numérique.
Arbre binomial à une période
Prenons l’exemple d’une option d’achat sur le groupe industriel Safran. Ce call européen porte sur une échéance de 6 mois, avec un prix d’exercice de 50€. Le cours de l’action est actuellement de 47€ et le taux d’intérêt sans risque pour une période de 6 mois est de 5% per annum. Les analystes qui suivent le titre pensent que celui-ci peut évoluer vers seulement deux prix dans un semestre : soit 55€ si les résultats financiers sont à la hauteur des espérances, soit 45€ si la compagnie n’atteint pas ses objectifs. Le call européen ne sera donc dans la monnaie que dans le premier cas de figure, et il revêtira alors une valeur de 55 – 50 = 5€. Dans l’autre cas, il termine hors de la monnaie et sa valeur sera nulle.
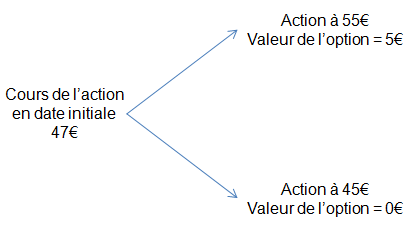
S’il n’existe aucune opportunité d’arbitrage, il est alors possible de constituer un portefeuille sans risque contenant à la fois une certaine quantité de l’action et une unité de l’option, de façon à ce que ce portefeuille ait une rentabilité égale au taux sans risque. Puisque le marché ne contient que ces deux actifs, il est dit « complet ». Combien faut-il d’unités Δ d’actions ?
Pour répondre à cette question, il suffit simplement de résoudre l’équation où un portefeuille contient Δ actions pour une option vendue, et de constater les deux valeurs finales potentielles du portefeuille. Premier scénario, Δ actions à 47€ sont achetées initialement et deviennent Δ actions à 55€ à l’échéance, avec un call ayant une valeur de 5€. Deuxième scénario, Δ actions à 47€ sont achetées initialement et deviennent Δ actions à 45€ à l’échéance, avec un call n’ayant aucune valeur puisqu’ayant terminé en dehors de la monnaie. Autrement dit :
D’où :
En détenant 0,5 action pour un call vendu, un portefeuille serait donc sans risque. Dans le cas où l’action grimperait à 55€, un tel portefeuille vaudrait 55 * 0,5 – 5 = 22,5€. Dans le cas où l’action descendrait à 45€, un tel portefeuille vaudrait 45 * 0,5 = 22,5€, une valeur équivalente à l’autre scénario, ce qui est bien ce que nous cherchions.
Ce portefeuille sans risque doit être actualisé, logiquement, au taux sans risque, afin de connaître sa valeur initiale. Celle-ci est de
Avec f comme valeur de l’option en date initiale, le portefeuille est ainsi constitué :
Ce portefeuille est égal à la valeur présente du portefeuille sans risque calculé précédemment. Autrement dit :
L’option d’achat ayant un prix d’exercice à 50€ et une maturité de 6 mois, calculé à l’aide de cet arbre binomial à une période, et sous réserve d’absence d’opportunité d’arbitrage, vaut 1,56€.
