Comment calculer la duration d’une obligation ? Définition & formule
Chaque détenteur d’obligation sait combien l’évolution des taux d’intérêts peut avoir un impact sur son portefeuille, et comment la duration peut l’aider à prendre des décisions pour la couverture de son risque de taux. De combien peut baisser la valeur d’une obligation à cause d’une hausse des taux d’intérêts ? Vaut-il mieux détenir des obligations à court terme ou à long terme pour être le moins dépendant possible d’une variation des taux d’intérêts ? Savoir comment calculer la duration d’une obligation est donc une étape essentielle de l’apprentissage de la finance et de l’immunisation de portefeuille.
Duration d’une obligation : définition & formule
La duration est en quelque sorte le temps d’attente moyen pour percevoir les flux d’une obligation, pondéré par leur valeur actualisée. Derrière cette définition absconse se cache en réalité une formule assez simple :
![]()
Avec :
– ti : nombre d’années du flux i
– ci : montant du flux i
– y : taux actuariel continu
On reconnaît au dénominateur l’expression du prix de l’obligation comme étant la somme des flux de celle-ci :
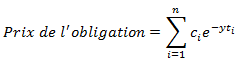
D’où :
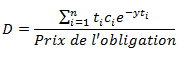
En dérivant le prix de l’obligation par rapport au taux actuariel, on trouve la relation suivante :
![]()
Duration d’une obligation : exemple numérique
Prenons une obligation 5 ans qui paie un coupon de 4% annuel, avec un taux actuariel de 3%. Le calcul de la duration de cette obligation va se faire en plusieurs étapes, en associant d’abord à chaque flux brut sa valeur actualisée, puis en calculant la part de ce flux actualisé dans la valeur actuelle de l’obligation. Il convient ensuite de multiplier cette part par le nombre d’années à attendre avant de percevoir le flux en question. La somme de chacun des produits va donner la duration de l’obligation.
|
Date |
Flux |
Flux actualisé |
Poids |
Date x Poids |
|
1 |
4 |
3,882 |
0,037 |
0,037 |
|
2 |
4 |
3,767 |
0,036 |
0,072 |
|
3 |
4 |
3,656 |
0,035 |
0,105 |
|
4 |
4 |
3,548 |
0,034 |
0,136 |
|
5 |
104 |
89,514 |
0,858 |
4,288 |
|
Total |
120 |
104,366 |
1,000 |
D = 4,639 |
Exemple avec la deuxième ligne :
– Flux actualisé = 4 * exp(-0,03 * 2) = 3,767
– Poids = 3,767 / 104,366 = 0,036
– Date * Poids = 2 * 0,036 = 0,072
On obtient finale une duration égale à D = 4,369.
Que se passerait-il avec un changement du taux actuariel, par exemple si celui-ci augmentait de 10 points de base ?
En appliquant l’équation donnée plus haut, on obtient :
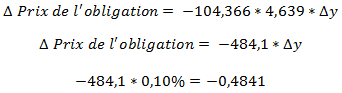
En d’autres termes, lorsque le taux actuariel augmente de 10 points de base, le prix de l’obligation diminue de 0,484.
Si l’on calculait le prix de l’obligation avec un taux actuariel de 3,10% au lieu de 3%, on obtiendrait :
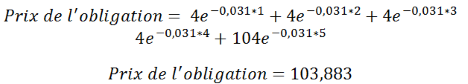
Ce qui donne une différence de prix 104,366 – 103,883 = 0,483. C’est bien ce que l’on a trouvé grâce à la duration, à deux chiffres près après la virgule.
Duration d’une obligation : limites
Le concept de duration n’est pas exempt de limites. Les principaux reproches faits à la duration sont les suivants
• La duration n’est précise que pour des mouvements faibles du taux actuariel (il ne s’agit que de la dérivée première du prix de marché de l’obligation par rapport au taux actuariel)
• La duration ne prend en compte que des mouvements parallèles de la courbe des taux d’intérêts, elle ne prend pas en compte des mouvements non-linéaires (ex. : redressement de la courbe sur le court terme uniquement, baisse de la courbe à long terme uniquement)
• La duration n’est pas fixe dans le temps, elle évoluera à mesure que l’on se rapproche et dépasse les échéances des flux, les réajustements de portefeuille doivent donc être réguliers
• La duration ne tient pas compte de la convexité des prix de l’obligation par rapport à un changement du taux actuariel (une baisse du taux actuariel fera augmenter le prix d’une façon plus importante qu’une dépréciation causée par une hausse du taux)
• La duration n’est centrée que sur le taux actuariel et le prix de l’obligation ; or, d’autres variables importantes telles qu’un changement de la qualité de la signature des émetteurs peuvent affecter de façon importante le prix d’une obligation


Je suis impressionné de la manière donc le cours est simple et bien détaillé. De ce fait y passerais toujours pour consulter. Merci
Qu’est ce que la convexité?
C’est la variation de la duration par rapport à la variation du prix de l’obligation sous-jacente.
Il y a une petite erreur dans la partie du calcul du prix de l’obligation avec un taux actuariel de 3,10% au lieu de 3%.
Le coupon reste le même (4%) et ce n’est pas 5%. En effet, 5% donnerait 108.443 alors que 4% donnerait le bon résultat que vous avez mis à la fin (103.8829).
Merci, l’erreur a été corrigée !