Comment calculer le taux de rentabilité interne d’un investissement ? Définition & exemple

Lors de l’évaluation de la pertinence d’un investissement, l’une des alternatives les plus courantes au calcul de la valeur présente est la recherche du taux de rentabilité interne (TRI). Est-ce une mesure plus adéquate ? Comment calculer le taux de rentabilité interne d’un investissement ? Formule & explications, exemple numérique à l’appui.

Taux de rentabilité interne : définition

La valeur présente et la rentabilité interne sont deux mesures très étroitement liées. En réalité, le taux de rentabilité interne est égal au taux d’actualisation qui produit une valeur actuelle nette nulle pour l’investissement. Par conséquent, le taux de rentabilité interne (TRI) peut être dérivé de cette équation :

Le tout premier flux (Flux₀) est égal au montant de l’investissement initial, et est donc négatif.

Chacun des flux futurs sera ramené à une valeur présente grâce à un taux d’actualisation identique, le taux de rentabilité interne.

Taux de rentabilité interne : exemple numérique

Prenons l’exemple d’un d’entrepreneur faisant l’achat d’un site internet afin d’appuyer ses ventes. Ce site lui coûte 100€ et devrait lui rapporter 115€ au bout d’un an. Quel est la rentabilité de cet investissement ? Il apparaît évident de dire que celle-ci est de 15%. Ce taux de 15% n’est autre que le taux de rentabilité interne de cet investissement. En utilisant la formule du TRI citée plus haut, on obtient :

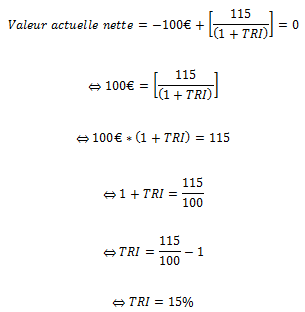
Imaginons désormais que ce site internet coûte toujours 100€ à l’acquisition, mais qu’il rapporte 70€ en première année, puis 70€ en deuxième année. On peut chercher à calculer le taux de rentabilité interne en résolvant l’équation suivante :

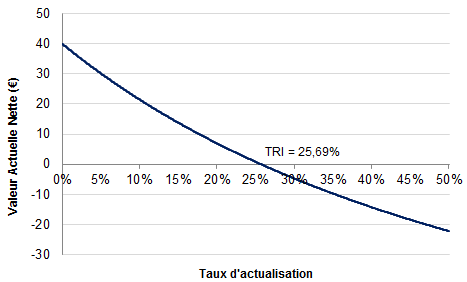
On obtient, par itération, un TRI égal à 25,69%. Si l’exigence de rentabilité de notre entrepreneur était inférieure à 25,69%, alors cet investissement serait attractif. Dans le cas contraire, il devrait rejeter cette acquisition.

La relation entre la valeur actuelle nette et le taux de rentabilité interne

A partir de l’exemple précédent (investissement de 100€, flux de trésorerie positifs de 70€ en année 1 et 70€ en année 2), il est possible de calculer les valeurs actuelles nettes qui seraient obtenues pour différents taux d’actualisation, dont le taux de rentabilité interne (TRI = 25,69%). Si le taux d’actualisation était nul, la valeur actuelle nette de cet investissement serait tout simplement de 70 + 70 – 100 = 40€. Plus le taux d’actualisation utilisé est fort, plus la valeur actuelle nette sera négative.

Les défauts du taux de rentabilité interne

Le taux de rendement interne n’est pas sans limites. Il s’agit d’une mesure imparfaite de comparaison entre plusieurs projets, qui ne doit pas se substituer au calcul de la valeur actuelle nette dans le processus de décision d’investissement.

La première limite tient à la nature des flux de trésorerie attendus. En effet, s’il s’avère que ces derniers sont positifs, puis négatifs, la résolution par itération du taux de rentabilité interne peut donner plusieurs valeurs. Et, si les flux négatifs sont fortement supérieurs aux flux positifs, il est tout à fait possible que la recherche du TRI soit impossible.

Par ailleurs, le simple calcul du TRI pour divers investissement pourrait conduire à décliner certaines propositions, que le calcul de la valeur actuelle nette, pour différents taux d’actualisation, contredirait.

Finance de Marché est un site d’information grand public, ayant pour vocation de partager les connaissances liées aux thématiques financières. Pour en savoir plus, pour des demandes de partenariat ou autre, n'hésitez pas à nous contacter.

Catégories : Entreprise, Finance, Généraliste | 11 commentaires