Taux d’intérêt composé classique et taux d’intérêt en composition continue
Même un non financier serait capable d’expliquer ce qu’est un taux d’intérêt. Communément appelé le « loyer de l’argent », le taux d’intérêt représente simplement ce que l’emprunter doit payer au prêteur. Un individu peut à la fois bénéficier d’un taux d’intérêt rémunérant son épargne lorsqu’il dispose son argent à la banque, ou payer un taux d’intérêt lorsqu’il emprunte de l’argent à sa banque. Les banques déterminent le taux d’intérêt qu’elles appliquent aux consommateurs, dans les deux sens, directement à partir des taux proposés par la banque centrale (taux de rémunération des dépôts ou « taux directeur » d’un côté, et taux de refinancement de l’autre).
Mais concrètement, comment mesurer un taux d’intérêt ? Quelle formule de taux d’intérêt retenir ? Qu’est-ce qu’un taux d’intérêt composé et un taux d’intérêt en composition continue ?
Taux d’intérêt composé classique
La plupart du temps, les taux d’intérêt sont exprimés de façon composée. Cela signifie que le capital produit un intérêt pour une période donnée, et que c’est à la fois le capital initial plus les intérêts de la première période qui donneront des intérêts pour la seconde période.
Imaginons qu’une banque vous propose un produit d’épargne à 5% par an.
Avec un taux de 6% en composition annuelle, cela signifie qu’à la fin de l’année, votre placement de 100 euros rapportera :
Le taux d’intérêt effectif est de 6%.
En revanche, toujours avec un taux de 6% mais en composition mensuelle, cela signifie que le taux d’intérêt mensuel est de 6%/12 = 0,5%, et qu’à la fin de l’année, votre placement de 100 euros rapportera :
Le taux d’intérêt effectif est donc de 6,17%.
La périodicité de composition des taux d’intérêts a donc une importance cruciale sur la valeur obtenue en fin de période. De façon générale :
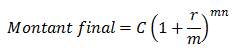
Avec :
C = Capital initial
r = Taux d’intérêt annuel
m = Fréquence de composition des intérêts (annuel = 1, semestriel = 2, mensuel = 12 etc.)
n = Nombre d’années
Avec cette formule de composition des taux d’intérêt, on peut constater l’effet de la périodicité sur le montant final obtenu à la fin d’une année :
| Fréquence de composition |
Valeur de 100€ à la fin de l’année |
| Annuelle (m = 1) |
106,000 |
| Semestrielle (m = 2) |
106,090 |
| Trimestrielle (m = 4) |
106,136 |
| Mensuelle (m = 12) |
106,168 |
| Hebdomadaire (m = 52) |
106,180 |
| Journalière (m = 365) |
106,183 |
Taux d’intérêt continu
L’autre convention parfois retenue pour le calcul des taux d’intérêt est la composition en continue. Celle-ci peut être imaginée comme une périodicité infiniment petite (m tend vers +∞). Cela équivaut à :
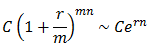
Avec :
e = nombre d’Euler ou constante de Néper (e ≈ 2,718).
Reprenons notre exemple pour une épargne rapportant 6% par an. Au bout d’un an, on obtiendrait donc :
Au bout de deux ans, on obtiendrait :
Le calcul d’options, le calcul des zéro-coupons ou bien d’autres calculs classiques en finance font intervenir des taux d’intérêts en composition continue, relativement plus facile à manier que des taux d’intérêts composés classiques.
Convertir un taux d’intérêt composé en taux d’intérêt continu
Si les taux d’intérêt en continu sont plus faciles à utiliser, le fait est que la majeure partie des taux d’intérêt sont exprimés en base composée. Il est donc important de savoir passer de l’un à l’autre.
Imaginons un taux d’intérêt avec composition annuelle de 6%. Quelle est le taux continu équivalent ?
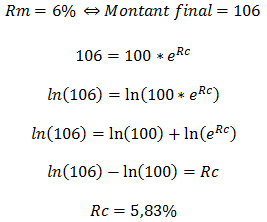
Avec :
Rc = taux continu
Rm = taux composé m fois
De façon générale, lorsque l’on cherche à trouver les équivalences pour les taux composés et taux continus, on peut utiliser l’équation suivante :
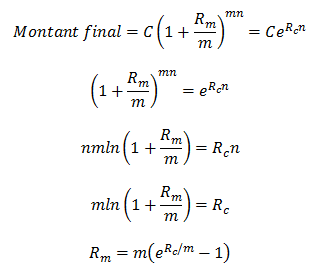


bonsoir, voila je cherche la démonstration en effet je sait que le taux équivalent de 12% annuel est 0,9489 mensuel.
donc si je place 1000 euros en taux annuel classique, j ai 1000*12%=120€ à la fin de l´année .
par contre en taux équivalent 120=quelque chose *12 période mais quoi comme calcul svp. j ai beau faire des calculs d intérêt composé je ne tombe jamais sur 120 ou approchant
Cordialement
Valeur future (Vf) = Valeur actuelle (Va) (1+i)^n , Donc 1000$*(1+0.009489)^12 = 1120$, d’où votre 120$ d’intérêt.
Bonjour
Les 120 correspondent uniquement aux intérêts. En réalité, la valeur acquise au bout de un an est 1000+120 soit 1120 euros.
Si tu veux utiliser le taux mensuel équivalent :
Le taux mensuel équivalent au taux annuel de 12% est 0,009488792935 exactement. Pour le retrouver, il suffit de résoudre l’équation si dessous afin d’obtenir le taux mensuel tm:
(1+ta)=(1+tm)^12
En utilisant ce tm, tu obtiens biens 1120 exactement :
Valeur au bout de un an en utilisant le taux mensuel
= 1000(1+ tm)^12 = 1 120
Good luck.
Salut,
Ici la résolution est simple : on fait C(1+i)^n – C
Et tu as les 120€
Application:
C=1000€ ; i=12/100 ; n=1.
1000(1+12/100)-1000 = 120€